library(tidyverse)
library(stat20data)
ggplot(data = penguins,
mapping = aes(x= body_mass_g)) +
geom_density()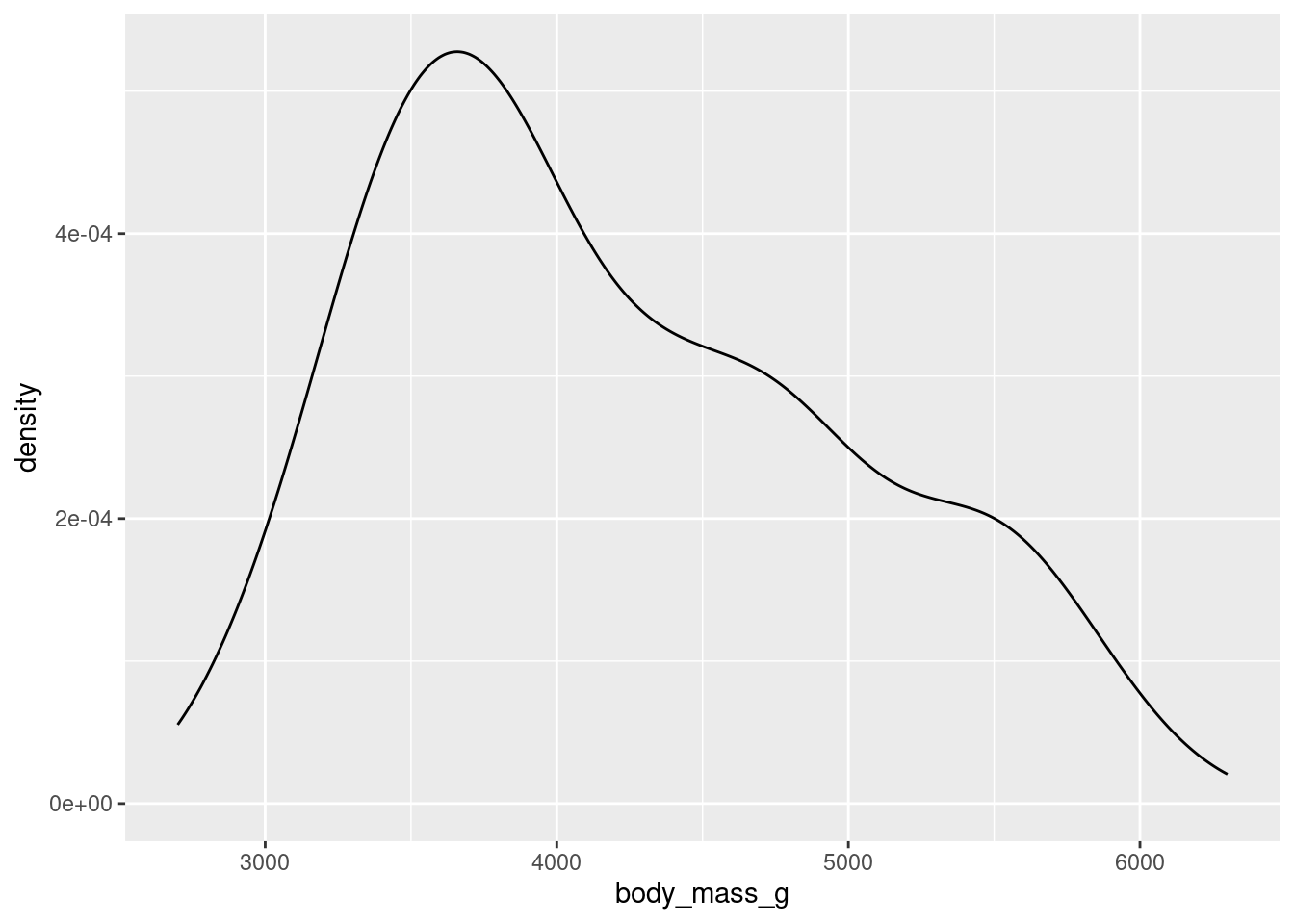
Seeing the forest for the trees.
Once you have your data in front of you, you’ve seen how we can form visual summaries with ggplot2. But how can we calculate numerical summaries? Furthermore, what if we are concerned about summarizing a portion of our data, like just one species of penguin at a time? We will answer these questions below, and introduce some new functions from the dplyr package (within the tidyverse library) along the way. We’ll also look at how factor() can come in handy while plotting.
If you are playing along in RStudio while reading these notes (which we strongly recommend!), be sure to start off by loading the two packages that are necessary for the tutorial by running the following code.
One example of a numerical variable we could have examine is the body mass of a particular penguin (measured in grams). Let’s calculate both a measure of center and spread for this variable.
To get an idea of what summaries we should pick, let’s revisit the density plot from earlier.

What we can glean from this figure is that the distribution of body masses across all species of penguin is skewed right. This means that, for instance, a more typical observation lies closer to 4000 grams than 5000 grams.
If we take an average, it is likely to be pulled to the right by the larger, but less typical, observations. The median observation, however, would be more resistant to this pull. Therefore, the median might be a nice choice for a measure of center. Similarly, since the IQR is initially constructed from the median, it will serve well here as a measure of spread.
Now, let’s calculate these values using summarize (you can also spell it summarise and it’ll work just the same). As is custom with dplyr functions, the first argument is the data frame you are working with. The subsequent argument(s) tell the computer what to do, referring to column names as needed. For summarize, each such argument is a calculation to perform.
# A tibble: 1 × 2
`median(body_mass_g)` `IQR(body_mass_g)`
<int> <dbl>
1 4050 1225The result of summarize is a new data frame (in this case, one row by two columns). Notice that the column names are kind of ugly - they are just the code used to make the calculation. You can rename these columns to whatever you like. Perhaps something like this:
# A tibble: 1 × 2
body_mass_median body_mass_IQR
<int> <dbl>
1 4050 1225Based on what we’ve found, the median here supports the claim we made above: that a typical penguin has a body mass closer to 4000 grams than to 5000 grams. The middle half of the penguins have body masses within a range of 1225 grams.
Let’s return to the bill length examine of a particular penguin, measured in millimeters. Here is the density plot for all of the data; for simplicity, earlier we showed you the plot for only the first 16 observations.
This plot is interesting. It appears we have a bimodal shape! While it’s tempting to state that the data is roughly symmetric and calculate an overall mean, we should first see if there are any other variables at play. It stands to reason that different species of penguin might have different anatomical features. Let’s add species to the mix by using the color aesthetic (see if you can code along)!
Aha! We now see that each penguin species has its own shape of distribution when it comes to bill length.
The example above demonstrates a very common scenario: you want to perform some calculations on one particular group of observations in your data set. But what if you want to do that same calculation for every group? For example, what if we’d like to find the average and standard deviation of bill length among each species of penguin separately?
This task - performing an operation on all groups of a data set one-by-one - is such a common data science task that nearly every software tool has a good solution. In the dplyr package, the solution is the group_by() function. Let’s see it in action.
Like most tidyverse functions, the first argument to group_by() is a data frame. The second argument is the name of the variable that you want to use to delineate groups. In this case, we want to group by species to calculate three separate mean/standard deviation pairs.
Now, assuming we roll with our new grouped_penguins data frame, we can use summarize() like we did before!
# A tibble: 3 × 3
species bill_length_mean bill_length_sd
<fct> <dbl> <dbl>
1 Adelie 38.8 2.66
2 Chinstrap 48.8 3.34
3 Gentoo 47.6 3.11From both the visuals and the numbers, we can see that Adelie penguins have much smaller bill lengths on average when compared to Chinstrap and Gentoo penguins. We also see that the Adelie distribution of bill lengths is less variable than the distributions of the other two species.
Finally, let’s return to the violin plot of bill lengths grouped by species of penguin (from the Notes page).
What if I wanted the Adelie violin to show up on the top of the graph? By default, the violin plot puts the level first in the alphabetical order on the bottom of the plot. Therefore, I need to reorder the levels of species to put Adelie at the top. This is where factor() will do the job!
We use the dplyr function mutate() to change a column, or to add a new column (which we will explore next week). Below, we overwrite the species column with a factor-ized version of itself, setting the order in which the species should always be displayed.
A few things are happening here:
mutate function is called, passing it our data frame (penguins) and one thing to do: change the species column to a factor, where the categories go in this particular order.penguins <- ...). This is common practice when you are cleaning up your data to be the way you want – you overwrite a dataframe with a new version of itself.Now, if we rerun the exact same code, the new category order is respected:
A summary of a summaries…this better be brief! Summaries of numerical data - graphical and numerical - often involve choices of what information to include and what information to omit. These choices involve a degree of judgement and knowledge of the criteria that were used to construct the commonly used statistics and graphics.